1. Puteri și radicali
- Puteri cu exponent întreg

Proprietățile puterilor cu exponent întreg:
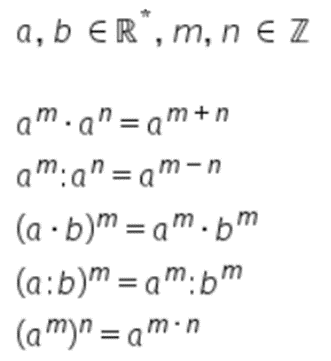
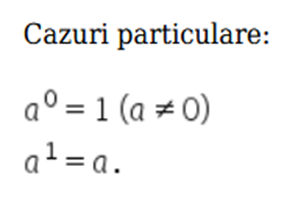
2. Radicali de ordin n
a) Radical de ordin n dintr-un număr real pozitiv

b) Radical de ordin impar dintr-un număr negativ
Dacă a < 0, și n ∈ ℕ*, n ≥ 3 este număr impar, atunci:

Proprietăți ale radicalilor de ordin n:
a) Radicalul unui produs
√ⁿ(a · b) = √ⁿa · √ⁿb, a, b ∈ [0, +∞), n ∈ ℕ* \ {1}.
Dacă n este impar, n ≥ 3, proprietatea este adevărată pentru orice a ∈ ℝ și b ∈ ℝ.
b) Radicalul unui raport
√ⁿ(a / b) = √ⁿa / √ⁿb, a ∈ [0, +∞), b ∈ (0, +∞), n ∈ ℕ* \ {1}.
c) Puterea unui radical
(√ⁿa)ᵐ = √ⁿ(aᵐ), a ∈ [0, +∞), m ∈ ℕ*.
Dacă n este impar, n ≥ 3, proprietatea rămâne adevărată și pentru a < 0.
d) Scoaterea unui factor de sub radical
√ⁿ(aᵐ · b) = aᵐ · √ⁿb, ∀ a ∈ [0, +∞).
e) Amplificarea, simplificarea unui radical
√ⁿa = √ᵏⁿ(aᵏ), ∀ a ∈ [0, +∞), k ∈ ℕ* (amplificarea).
√ᵏⁿ(aᵏ) = √ⁿa, a ∈ [0, +∞), k ∈ ℕ* (simplificarea).
f) Compunerea radicalilor
√ᵐⁿa = √ᵐ(√ⁿa), ∀ a ∈ [0, +∞).
g) Compararea radicalilor
Dacă a, b ∈ [0, +∞), atunci √ⁿa ≤ √ⁿb ⇔ a ≤ b.
Operaţii cu radicali:
1. Înmulțirea radicalilor
√ⁿa · √ⁿb = √ⁿ(ab), a, b ∈ ℝ.
√ⁿa₁ · √ⁿa₂ · … · √ⁿaₖ = √ⁿ(a₁a₂…aₖ), aᵢ > 0, i = 1, n.
2. Împărțirea radicalilor
√ⁿa / √ⁿb = √ⁿ(a / b), a, b ∈ [0, +∞), b ≠ 0.
3. Ridicarea la putere
(√ⁿa)ᵐ = √ⁿ(aᵐ), a ∈ (0, +∞), m ∈ ℤ.
4. Scoaterea unui factor de sub radical
√ⁿ(aᵏb) = aᵏ · √ⁿb, a, b ∈ [0, +∞).
5. Înmulțirea unui radical cu un întreg (introducerea factorilor sub radical)
a√ⁿb = √ⁿ(aⁿ · b), a, b ∈ [0, +∞).
6. Radicali de ordin _n_ dintr-un radical
√ᵐ(√ⁿa) = √ᵐⁿa, a ∈ [0, +∞).
7. Raționalizarea numitorilor
• A raționaliza numitorul unei fracții înseamnă a elimina radicalii de la numitor.
• Două expresii se numesc conjugate dacă produsul lor este o expresie fără radicali.
• Pentru a raționaliza numitorul unei fracții se amplifică fracția cu conjugata expresiei de la numitor.
a) Numitorul este un radical.
Dacă numitorul este √ⁿaᵏ, a > 0, k < n, atunci fracția se amplifică cu √ⁿaⁿ⁻ᵏ și numitorul devine:
√ⁿaᵏ · √ⁿaⁿ⁻ᵏ = a.
b) Numitorul este de forma (√a ± √b), a, b > 0.
3. Puteri cu exponent raţional
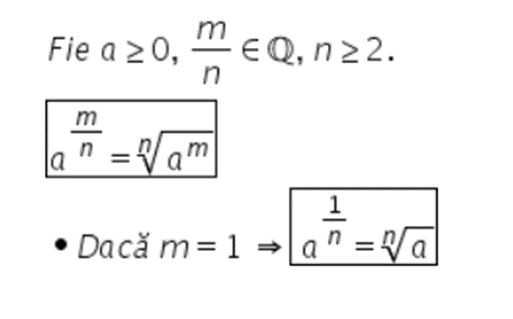
Proprietățile puterilor cu exponent rațional (a, b >0):
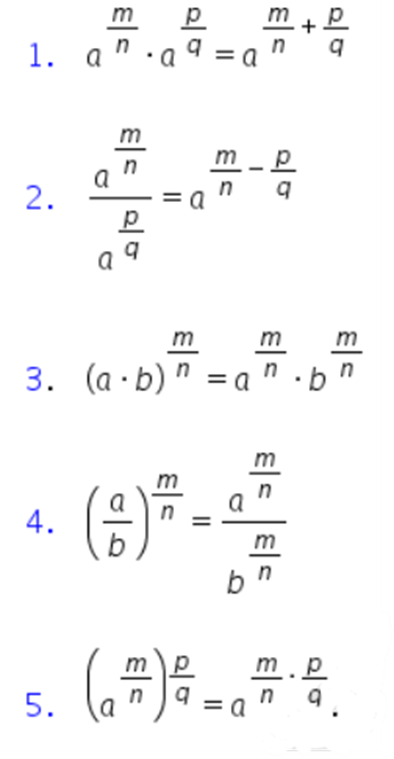
4. Logaritmul unui număr real pozitiv
Fie a > 0, a ≠ 1 și N > 0 un număr real pozitiv. Logaritmul în baza a al numărului real pozitiv N este exponentul la care trebuie ridicat a pentru a obține numărul N.
Se notează:
logₐN = x ⇔ aˣ = N, cu a > 0, a ≠ 1, N > 0.
Proprietăți și operații cu logaritmi:
Pentru orice a > 0, a ≠ 1, b > 0, b ≠ 1, x > 0, y > 0, avem următoarele proprietăți:
1. Logaritmul produsului: logₐ(x · y) = logₐx + logₐy
2. Logaritmul câtului: logₐ(x / y) = logₐx – logₐy
3. Logaritmul unei puteri: logₐ(xⁿ) = n · logₐx, ∀ n ∈ ℝ
4. Formula de schimbare a bazei: log_b x = logₐx / logₐb
5. Logaritmul unui invers: logₐ(1 / x) = -logₐx
Cazuri particulare
logₐ1 = 0
logₐa = 1
logₐ(aⁿ) = n
Elevi: Stroiescu Diana, Lăcraru David, Petrovanu Paul