CUPRINS
- Forma algebrică a unui număr complex. Operații cu numere complexe;
- Numere complexe conjugate. Modulul unui număr complex;
- Interpretarea geometrică a numerelor complexe;
- Rezolvarea în C a ecuației de gradul 2 cu coeficienți numere reale. Ecuații bipătrate;
- Forma trigonometrică a numerelor complexe. Operații
INTRODUCERE
La început, omul nu știa decât de existența numerelor naturale. Pentru a efectua scăderi a fost necesară creearea mulțimii de numere negative. Pentru a împărți unele numere, s-a creeat mulțimea Q și au apărut și fracțiile. Numerele iraționale au apărut când s-a încercat scoaterea rădăcinii din numere care nu sunt pătrate perfecte. Apoi, s-a încercat rezolvarea ecuațiilor de gradul al II-lea cu Δ negativ, și pentru asta au trebuit să creeze un număr egal cu √-1. Și acesta era i (iota).
Definiția numerelor complexe:
Un număr complex este definit ca fiind de forma a + bi, unde a și b sunt numere reale, iar i este unitatea imaginară, cu proprietatea că i² = -1. Această definiție permite manipularea și operarea cu numere care nu au reprezentare pe axa numerelor reale.

Din ce este format numărul complex?
Numărul complex se mai numește și număr imaginar. Acesta are o parte reală și o parte imaginară, de exemplu z=14+25i. Mulțimea numerelor complexe include și mulțimea numerelor reale și se notează cu C.
Denumirea de număr imaginar a fost folosită încă din secolul al XVII-lea. Matematicianul Rafaele Bombelli a dezvoltat o teorie a acestora (1572), iar mai apoi studiul a fost dezvoltat de Bernoulli, Euler și Gauss.
1. Forma algebrică a unui număr complex. Puterile lui i
C=mulțimea numerelor complexe.
C={z | z=ai + b; a, b ∈ℝ}
Z=a*i + b forma algebrică a unui număr complex.
A=Re(z) partea reală a unui număr complex.
B=Im(z) partea imaginară a unui număr complex.
Ex:1. z=4i+3; Re(z)=3, Im(z)=4
2. z=4i; Re(z)=0, Im(z)=4
Egalitatea a două numere complexe z şi z’: a + ib =a’ + ib’; a=a’ şi b =b’
Operații:
- Adunarea
z1+z2=a1+b1i+a2+b2i=(a1+a2) + (b1+b2)i
Are următoarele proprietăți:
- asociativă
- comutativă
- admite ca element neutru pe 0=0+0i
- orice număr complex z= a + bi admite un opus–z =–a– ib.
- opusul lui z=a+bi este −z=−a−bi
2. Scăderea
z1-z2=(a1+a2)-(b1+b2)i
3. Înmulțirea
z1*z2=(a1+b1i) + (a2*b2i)=a1*a2+a1*b2i+b1i*a2+b1*b2i2=(a1*a2-b1*b2) + (a1*b2+a2*b1)
4. Împărțirea
z1/z2=a1+b1i/ a2+b2i= a1*a2-a1*b2i+b1*a2-b1*b2i2/a1*a2+b1*b2+ (b1*a2-a1*b2)
2. Numerele complexe conjugate. Modulul unui număr complex
Un număr complex nu apare pe axa obișnuită a numerelor, deci nu poate fi ordonat crescător sau descrescător.
Dacă z=a+bi, atunci |z|= √a2+b2, iar z>0.
Conjugata unui număr complex se notează cu z=a-bi. Aceasta are același modul ca z=a+bi. În plus, z*z=|z|2 și |z|2 = |z2|.
Deoarerce √-1=i, atunci i2=-1, i3=-i și i4=1. Funcția f:R->C; f(x)=ix este periodică pe t=4.
- Conjugatul unui număr complex este obținut prin schimbarea semnului părții imaginare, având forma a – bi, unde a și b sunt numere reale. Această operație este utilă în simplificarea calculului împărțirii numerelor complexe.
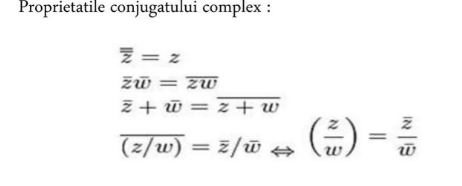
- Modulul unui număr complex, notat |z|, este distanța de la originea planului complex la punctul corespunzător numărului complex. Se calculează folosind formula |z| = √(a² + b²), unde a este partea reală și b partea imaginară.
- Reprezentarea grafică a numerelor complexe se face pe un plan numit planul complex, unde axa orizontală reprezintă partea reală, iar axa verticală partea imaginară. Această reprezentare ajută la vizualizarea operațiunilor cu numere complexe, cum ar fi adunarea și înmulțirea.

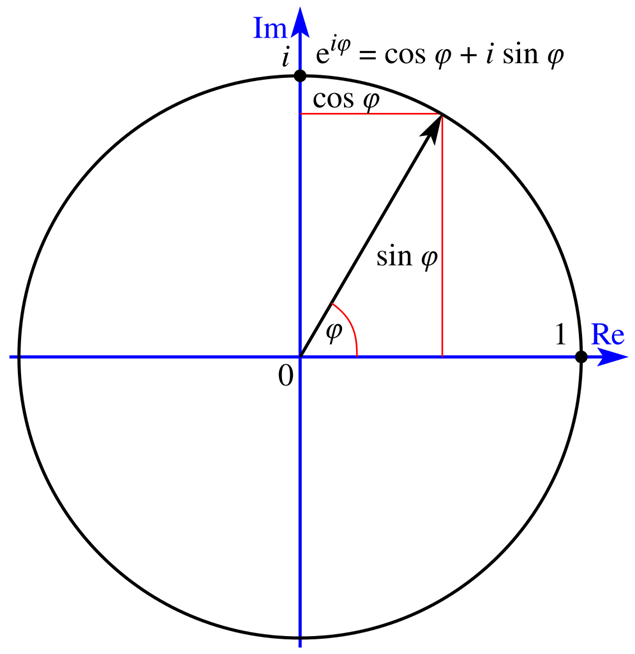
Identitatea lui Euler
Considerată cea mai frumoasă formulă de matematică, aceasta spune că eiπ=-1. Dar de ce? Aceasta derivă din formula lui Euler, care spune că eix=cos(x)+i sin(x). Dacă luăm x drept π, atunci avem eiπ=cosπ+i sinπ, care va fi egal cu cos (180o)+i sin (180o), adică -1+0=-1, deci acest lucru demonstrează faptul că eiπ=-1.
3. Interpretarea geometrică a numerelor complexe
- Fie z aparține C , z=a+bi aparțin R si i2=-1. Fiecărui număr complex îi corespunde un unic punct M(a,b) din plan și reciproc, fiecărui punct M din plan îi corespunde un singur număr complex z=a+bi. Punctul M(a,b) asociat lui z=a+bi se numește imaginea geometrică a lui z. Numărul complex z corespunzător punctului M se numește afixul punctului M si se scrie M(z).
- Interpretarea geometrică a modulului nr. complex. Daca z=a+bi, atunci |z|=OM=
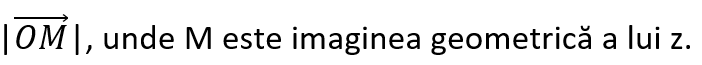
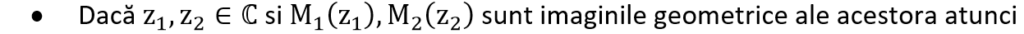

Cazuri particulare :
- Dacă M este mijlocul segmentului [M1 M2] atunci zM=z1+z2/2
- Afixul centrului de greutate G al triunghiului ABC în funcție de afixele vârfurilor triunghiului este k=(zA+zB+zC)/3
- Punctele A, B ,C cu afixele zA,zB,zC sunt coliniare dacă și numai dacă:
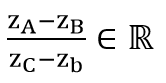
4. Rezolvarea în C a ecuației de gradul 2 cu coeficienți numere reale. Ecuații bipătrate
Ecuația de forma ax4+bx²+c=0 unde a,b,c∈R, a≠0, x – variabilă, se numește ecuație bipătrată. Prin substituția x2 = t (atunci x4 = t2) ecuația bipătrată se reduce la o ecuație de gradul al doilea.


5. Forma trigonometrică a numerelor complexe. Operații

Aplicatii in viata de zi cu zi
Acestea sunt utilizate în multe domenii, precum matematica și ingineria, oferind soluții la probleme care nu pot fi rezolvate cu numere reale. În domeniul fizicii, aceste numere complexe sunt regăsite în mecanică, fizica teoretică,hidrodinamică.
Transformarea Fourier-în ingineria electrică este utilizată pentru a analiza diferite tensiuni și curenți.
În matematică transformata ,Fourier (numită astfel după matematicianul și fizicianul Joseph Fourier) este o operație care se aplică unei funcții complexe și produce o altă funcție complexă care conține aceeași informație ca cea originală.
Numerele complexe sunt mai ușor de înțeles dacă sunt reprezentate într-un grafic. Dacă desenăm o linie și un unghi cu o anumită direcție obținem o reprezentare grafică a unui număr complex, cunoscută sub numele de vector.
Exerciții rezolvate
- z1=3+4i și z2=1-2i; a) z1+ z2=? b) z1– z2=?
a) z1+ z2=(3+4i)+(1-2i)=(3+1)+(4i-2i)=4+2i
b) z1– z2=(3+4i)-(1-2i)=(3-1)+(4i+2i)=2+6i
2. z1=2 – 5i și z2=1 – 6i
a) z1+ z2=? b) z1– z2=? c) z1*z2=?
a) z1+ z2=(2 – 5i) + (1 – 6i) = (2 + 1) + (-5 -6)i = 3 – 11i
b) z1– z2=( 2 – 5i) – (1 – 6i) = (2 + 1) + (-5 – (-6))i = 1 + i
c) z1*z2=( 2 – 5i) x (1 – 6i) = (2 x 1 – (-5)(-6)) + (2 x (-6) + (-5) x 1)i = -2i
Elevi : Neagu Carolina, Vasiliu Ana, Terecoasă Sabina, Apostol Teodora, Ulieru Delia, Duță Cristina, Lungu Rareș